The National Council of Teachers of Mathematics (NCTM) released a position statement related to procedural fluency and that is the focus of this post. The NCTM has the following information shared on its website:
is the world's largest mathematics education organization
advocates for high-quality mathematics teaching and learning for each and every student (yes these bolded words will come back later)
provides guidance and resources for the implementation of research-informed and high-quality teaching that supports the learning of each and every student in equitable environments (see above)
advances a culture of equity where each and every person has access to high-quality teaching empowered by the opportunities mathematics affords (LOVE this statement)
provides community and resources to engage and listen to members in order to improve the teaching and learning of mathematics (LOVE this statement)
engages in advocacy to focus, raise awareness, and influence decision makers and the public on issues concerning high-quality mathematics teaching and learning (see above)
Where are we going with this post?
What is included in the NCTM’s position statement?
What is the NCTM’s working definition for fluency and how do other definitions compare/contrast?
What is the relation between conceptual knowledge and procedural knowledge?
How can we assess fluency?
What does all this jawn mean for teaching? (remember good ol’ Art Dowdy)
NCTM Position Statement
Through their twitter handle, the NCTM released 4 graphics on Twitter to disseminate key points related to their position statement along with a link to the actual document.
The statement has a couple aspects to unpack. It includes an introduction followed by a series of declarations (they used the term declaration not me, if you do not believe me here is the link again).
They suggest fluency has a definition that is correct (theirs) and some that are incorrect. An incorrect definition would fit this idea, “remembering facts and applying standard algorithms or procedure.”
Declaration #1 “Conceptual understanding must precede and coincide with instruction on procedures”
Declaration #2 “Procedural fluency requires having a repertoire of strategies”
Declaration #3 “Basic facts should be taught using number relationships and reasoning strategies, not memorization”
Declaration #4 “Assessing must attend to fluency components and the learner. Assessments often assess accuracy, neglecting efficiency and flexibility”
Procedural Fluency Definition
The NCTM’s definition for procedural fluency is “skill in carrying our procedures flexibility, accurately, efficiently, and appropriately.” They cite 6 references to support this definition, let us take a look.
Two of the citations are documents the organization had produced previously (NCTM 2014 and NCTM 2020). These documents do not provide a unique definition but instead refer to the next three citations (see below).
Three of the citations all are from documents produced by the National Research Council (2001; 2005; 2012). The NRC (2001) Adding it Up is the initial proposal of this definition.
One citation (Star, 2005) was from an article I would argue EVERY math teacher should read. The article provides an in depth discussion on defining procedural knowledge and makes a case for why flexibility was at that time an under-discussed and important component to build a depth of procedural knowledge. The missing link here is what it would mean to demonstrate fluency with procedures.
To quickly summarize, 5 supporting citations for the correct definition all reference really just 1 proposed definition by the NRC in Adding it Up. The other citation (Star, 2005) builds an argument that to have a depth of procedural knowledge - flexibility is important.
“Oh, wow I am surprised the only proposed (and apparently correct) definition for fluency is from the National Research Council”
In the words of Lee Corso, “Not so fast my friend.”1
If the NCTM had stuck with defining procedural knowledge I might not have even included this section. But they specifically aimed to define procedural fluency and with their citation choice above and corresponding description ignored an ENTIRE literature base. This is unsurprising. The NRC definition they used was comprised of a committee that did not include representation from the fields of special education, school psychology, or behavior analysis. The NCTM board who approved the position statement also does not include representation from special education, school psychology, or behavior analysis. The NCTM states they focus on high-quality instruction and learning for each and every student - but have limited to no input from individuals with expertise in supporting the math development of students with math difficulty, math disability, or other disabilities.
One definition for fluency not considered by the NCTM program can be found here. The author (Carl Binder) has devoted a significant time investigating what it means for people to build behavioral fluency. In the article the following quote is provided,
For example, when asked to list associations with the phrase behavioral fluency, one group produced responses that included easy to do, mastery, really knows it, flexible, smooth, remembered, can apply, no mistakes, quick, without thinking, automatic, can use it, not tiring, expert, not just accurate, and confident (p. 164).
I see the author’s aim to highlight, colloquially many people have a prior schema they pull from when they hear the term fluency and interpret what this would mean in various situations. It is worth noting there are many overlaps with this concept of being fluent and what the NCTM defined as procedural fluency.
So what differs? The consideration of RATE of performance (speed + accuracy) is integral in informing our understanding of where a person currently sits within their aim to build fluency in a skill. If we tie back to the NCTM’s definition: “skill in carrying our procedures flexibility, accurately, efficiently, and appropriately” we want to really focus on those bolded attributes. The flexibility aspect for building a depth of procedural knowledge is critical!
Thus, the NCTM stating, “remembering facts and applying standard algorithms or procedures” is an incorrect definition for fluency is not accurate. A learner who is fluent in a specific skill within math should be able to do those things ALONG with the demonstrating flexibility in knowing when, how, and which situations to apply this knowledge.
Declaration #1 Conceptual understanding must precede and coincide with instruction on procedures
On the bird app, (jk) this declaration received lots of critiques with two primary themes: (a) the use of precede and coincide in the same sentence and (b) the actual research supporting this claim.
Did the chicken precede or coincide with the egg?
I actually hadn’t considered the confusion with the statement using precede and coincide. My interpretation of the statement was the NCTM is declaring that conceptual knowledge should be taught first (i.e., precede part) and then once instruction on procedures occurs, there still needs to be a focus on conceptual knowledge (i.e., coincide part).
Evidence for Concept before Procedure?
I do not want to spend too much time on this. But it does appear to be a pretty glaring oversight to include a citation to this paper by Rittle-Johnson and colleagues (2015) to support the declaration. Here is a direct quote from the paper (p. 593).
Although the relations between the two types of knowledge are bidirectional, it may be optimal for instruction to follow a particular ordering. The prevalent conceptual-to-procedural knowledge perspective asserts that instruction should extensively develop conceptual knowledge prior to focusing on procedural knowledge (Grouws and Cebulla 2000; NCTM 1989, 2000, 2014). Unfortunately, we could not find empirical evidence to directly evaluate claims for an optimal ordering of instruction. Given the bidirectional relations between conceptual and procedural knowledge, we suspect that there are multiple routes to mathematical competence and that a conceptual-to-procedural ordering is not the only effective route to mathematical competence. (I added the bolded words)
One other comment and then we can move on. The NCTM state, “Conceptual foundations lead to opportunities to develop reasoning strategies, which in turn deepens conceptual understanding; memorizing an algorithm does not.” Memorizing an algorithm without ANY instruction focused on why it works, when to apply it, and how it may relate to other strategies is poor teaching. But claiming that having the procedures of an algorithm stored in long term memory (i.e., it has been memorized) to then refer to when critiquing, inspecting, thinking about concepts to deepen conceptual knowledge as a bad/pointless idea just does not make sense.
Declaration #2 Procedural fluency requires having a repertoire of strategies
I agree here (despite the tone used to discuss algorithms). The one caveat I’d add is in practice this recommendation can run the risk of surface level instruction. For example, if we consider double digit multiplication I have seen the following taught in schools (a) area model, (b) partial products (2 different ways), (c) lattice, and (d) standard algorithm. To build fluency a learner must engage in a sufficient amount of strategically designed practice opportunities across time. My concern is teachers often are pressured by the breadth of the content standards for their grade level which impacts pacing guides. Thus, introducing 3, 4, or 5 different “strategies” without sufficient practice opportunities will impact the likelihood learners will actually become fluent in any strategy.
Declaration #3 Basic facts should be taught using number relationships and reasoning strategies, not memorization
Memorization is bad for math. That is my takeaway. We obviously use memorization all the time for daily life things and that is fine. Here are some examples:
our birthdays
birthdays of significant people in our lives
our phone number
our home address
our social security number
our license plate number
But math is different and we should not use memorization. But we can use it for other content. For example, in early literacy here are some things kids memorize:
Letter names
Letter sound correspondences
Digraph sound correspondences
Phonics patterns (e.g., CVCe for example how do I read BAKE)
It is the outright refusal to acknowledge memorization is useful that is the problem with me. Of course, teaching number relations is important! For example, if I present 3 + 9 to my 5 year old daughter I want her to know the following:
I can start at 3 and count up 9
I instead can use the commutative property of addition and more efficiently start at 9 and count up 3
I can use my knowledge of making 10, and decompose 3 into (2 + 1) and then do (9 + 1) + 2
All of these are highlighting important concepts related to the concept of addition. All of these are also great back up strategies if a child is presented 3 + 9 and it is not known – they can actually solve it! But stating that a child should not engage in any instructional activities that promote memorization the three term contingency 9-3-12 are paired is problematic. A learner pairing this three term contingency can efficiently do the following
3 + 9 = 12
9 + 3 = 12
12 - 3 = 9
12 - 9 = 3
I feel the need to re-emphasize this point - I AM NOT ADVOCATING FOR ONLY DOING INSTRUCTIONAL ACTIVITIES FOCUSED ON MEMORIZING FACTS. Rather, instruction focused on students retrieving known information would be situated within a comprehensive math instructional diet. Here are a couple critical points related to retrieval practice with math facts:
Distribution across time enhances outcomes. For example, if you plan to do 4 minutes of practice a day you’ll be better off doing 2 min practice in morning and 2 min practice in the afternoon versus doing one, 4 min practice session. Here is one article that highlights this.
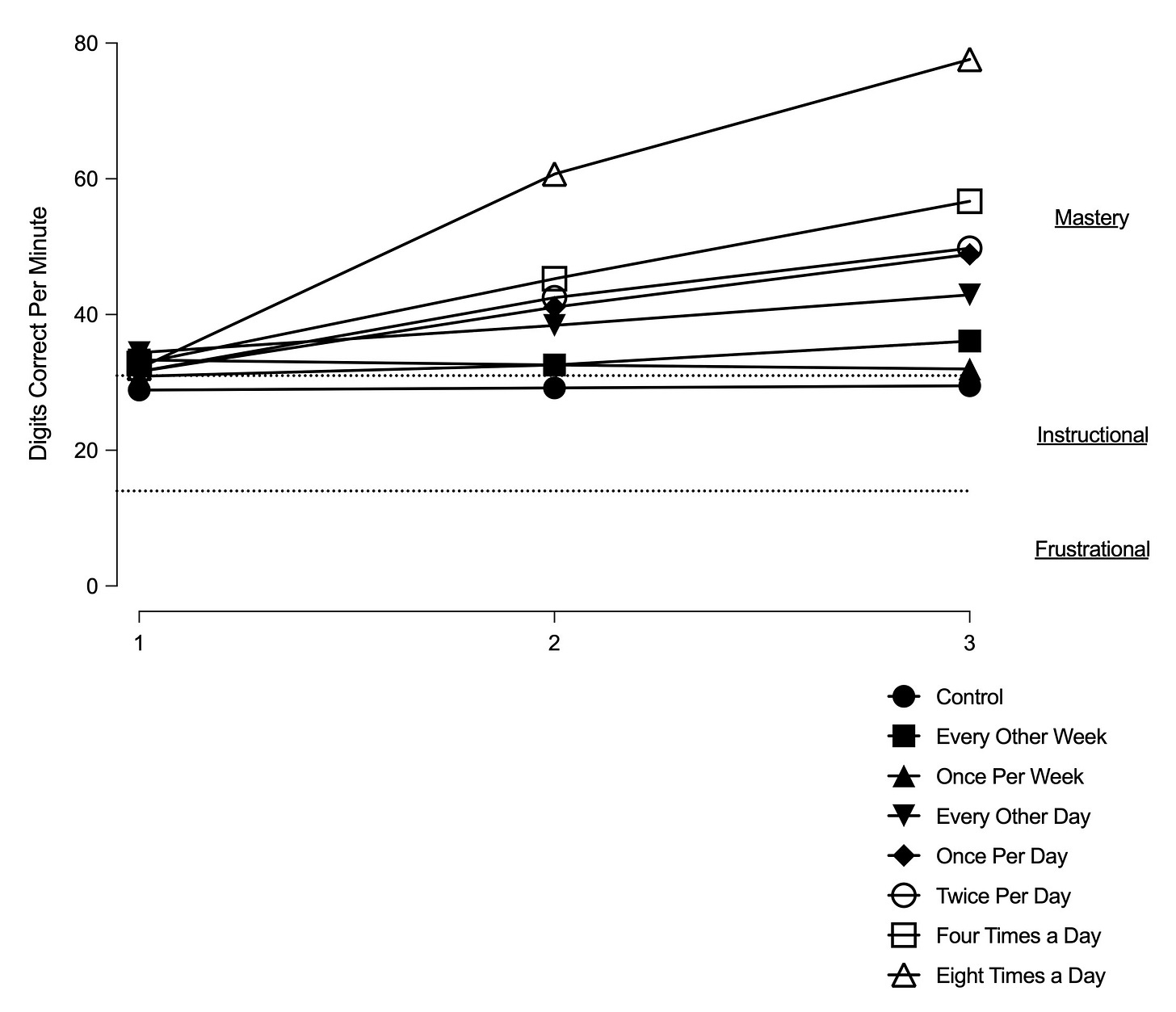
Practice has to occur DAILY. Doing practice once every two weeks, once per week, or every other day (e.g., 3 times per week) all saw less effects than daily2. This study found only 2 min of daily practice led to meaningful gains - although you can see 8 min and 16 min of practice outperformed 2 min and 4 min of daily practice. But the key here is it only would take 2 to 4 min of time, which is 3.33% to 6.66% of an entire 60 min math block, to likely observe meaningful gains on fact fluency if good instruction is provided. See Figure below3 .
Declaration #4 Assessing must attend to fluency components and the learner
This declaration correctly identifies that accuracy alone is a poor metric! If you want a deeper discussion read this (please forgive me for citing an article I was a co-author on). For a very simple explanation consider this:
Student 1 can solve problems with two addends that sum to 10 (e.g., 4 + 6; 3 + 4) accurately (100%) but each item takes them approximately 6 to 7 seconds because they are using a counting procedure.
Student 2 can solve problems with two addends that sum to 10 accurately (100%) but each item takes them approximately 1 to 2 seconds because they are retrieving from memory.
If we only use an assessment procedure that captures a metric of accuracy, we would conclude both students are equivalent in their knowledge. Yet, this is clearly not sure - one is efficiently pulling from memory the other is currently strategy-bound.
Yay, we agree! We can conclude this post?
Not quite yet, the NCTM states “Timed tests do not assess fluency and can negatively affect students, and thus should be avoided.”
As we already discussed at the beginning of this section, speed + accuracy (i.e., rate data) does capture components of fluency. Thus, focusing on how quickly a child can perform a skill is integral to measure fluency. This can be done via timed practice or measuring latency of responding through another assessment approach (i.e., when I present 3 + 4, I can count how long until a child says 7 - this is latency).
The negatively affect students statement is one I really resonate with. We must consider the social validity4 of our instructional practices based on the goals we set for students, the procedures we are using as part of instruction, and the outcomes we observe. One concern I have is timed practice has been used terrible in practice. I have used the following mock scenario in class for students to critique:
A teacher administers a math multiplication fact sheet to all students in the class. All students get the same exact sheet. Before the teacher starts the timer they say something like, "It is important to master our math facts. If you get below [X] correct then we will spend the first 5 minutes at recess practicing." As students work on the sheet you see students quickly slapping their pencil down and flipping their paper over to signify they finished. Other students quickly look at them and frantically get back to their sheet. As the timer rings the teacher yells, "Times up, trade with your shoulder partner." The teacher has students exchange sheets with a peer. As the teacher reads off the answers the peer scores the sheet. Later that day the teacher updates everyone's score on a bulletin board that is visible for everyone to see.
I think a lot of the pushback on timed assessments include one of the elements from the context above. So let’s discuss the problems:
In many situations, having all students in a class practice the same exact items under timed conditions is going to be inappropriate. For some students, these skills are likely still in the frustrational range (i.e., students still make lots of errors). This would be a punishing task. It will be critical to differentiate the specific math skills (or items) we are asking students to answer under timed practice.
The teacher directions for the task phrased this as a high-stakes situation. This will enhance the likelihood some students may experience elevated levels of anxiousness. There is actually research showing that altering directions can impact participant responding for oral reading fluency tasks (Christ et al.; Colón & Kranzler) but not always (Taylor et al). But this really seems like common sense, keep it informal.
Also, the teacher is removing a an activity that is likely reinforcing for many children and replacing it with math practice. This likely over time would increase the likelihood math will become an aversive activity.
The students racing against one another turns this into a competitive, norm comparison situation. This can impact student overall self-esteem and self-concept. First, each student needs to have enough items to practice during the time limit (e.g., 1 min, 2 min, 3 min) so they do not finish before the time limit is reached. This ensures students are not wasting time not being able to practice and second avoids the comparison situation above.
The peer grading once again is just terrible idea in this situation. It pivots on norm comparison situations rather than students focusing on their own improvement in their fluency from practice session to practice session.
Posting scores. Also terrible idea. I do not think I need to add more here. The goal should be an individual student aiming to beat their own previous score. All about individual student progress (no need to focus on anyone else in the class, just my own previous performance). Students can graph their own data (sticker chart, bar chart, time series graph) to see their performance practice session to practice session. If good instruction is being provided across time with enough dosage, they will be able to see their hard work pay off in growth!
The NCTM provides three alternative options: interviews, observations, and written prompts. Evaluating student knowledge is pretty dang difficult to do well. Reliability and validity are properties that we must consider when evaluating if information we capture appears to be of sufficient quality to interpret and then actually use for decision-making.
Listening to students verbalize their math thinking and reasoning is a critical instructional tool. Observing students engage in math tasks can provide useful information about how they attack a problem, communicate or work with peers, and use tools (e.g., number lines, manipulatives) to engage in thinking. Engaging with math through written expression is a higher level, cognitively demanding task. Writing is not only a medium that is used frequently to assess knowledge, but has been shown to be a useful instructional component to promote learning (Graham and colleagues). This all three recommendations can be useful as part of a teacher’s instructional repertoire!
Yet, as the go-to approach to evaluate fluency - I’d have major reservations. First, conducting a 3, 4, or 5 min interview with every student in a class would take A LONG TIME. This would severely limit the frequency in which a teacher could get usable information on student development in their fluency for specific math skills. Second, interviews are so language heavy we may end up picking up “construct irrelevant variance.” Meaning we might begin to measure how well a student can verbalize their thoughts versus their actual fluency in the math skill. Third, obtaining consistent conclusions person to person conducting the interview (or observation) is likely to be a much harder threshold to achieve - this inconsistency for evaluation is not ideal. A potential alternative is the use of curriculum-based measures5, which have demonstrated pretty strong utility for monitoring student math growth for screening and progress monitoring decisions (Nelson et al).
Conclusion
The NCTM Position Statement highlights flexibility is important. This is an important area of further investigation to (1) identify what specific types of “flexibility” are more or less important for later math achievement, (2) identify how to measure flexibility well, (3) identify instructional strategies that promote flexibility, and (4) identify when to target flexibility (i.e., where in the student’s current knowledge is it most advantageous to target flexibility).
Unfortunately, there are many suggestions included in the position statement that are head scratching. I’ll keep an optimistic view and hope future content aligned with this position statement may provide further clarification - but I will not hold my breath.
Not to brag or anything (yes this is definitely me bragging but perhaps….humbly), but I was able to slip this quote into a peer-reviewed paper! Honestly, highlight of my career (see here).
The NCTM cited Baroody and colleagues (2016) in this section. The “drill group” in this study practices 2 times per week, 30 min total session time. The “drill group” as designed for this study does not fit the procedures I am suggesting would be beneficial for learning. For example, we must select facts students know but are slow with, practice should be short and distributed across the day, practice should be daily, and building in motivational components for students is critical.
These data are presented in Figure 2 (p. 6) of this article. I digitized the data and recreated the graph to (a) avoid copyright issues and (b) to add the suggested cut points for determining skills in a learner’s frustration range, instructional range, or mastery range.
If you want to read a little on this, here is a preprint from one of the leading researchers investigating social validity in single-case research.
This is already really long so I don’t want to give CBMs a short two sentence description because they deserve better. I plan to put together a post all about CBMs in the near future!



